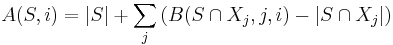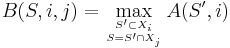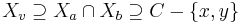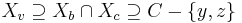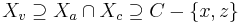Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph. The treewidth measures the number of graph vertices mapped onto any tree node in an optimal tree decomposition. While it is NP-hard to determine the treewidth of a graph, many NP-hard combinatorial problems on graphs are solvable in polynomial time when restricted to graphs of bounded treewidth.
In machine learning, tree decompositions are also called junction trees, clique trees, or join trees; they play an important role in problems like probabilistic inference, constraint satisfaction, query optimization, and matrix decomposition.
The concept of tree decompositions and treewidth was originally introduced by Halin (1976). Later it was rediscovered by Robertson & Seymour (1984) and has since been studied by many other authors[1].
Contents |
Definition
Intuitively, a tree decomposition represents the vertices of the given graph as subtrees of a tree, in such a way that vertices are adjacent only when the corresponding subtrees intersect. Thus, the graph forms a subgraph of the intersection graph of the subtrees. The full intersection graph is a chordal graph.
Each subtree associates a graph vertex with a set of tree nodes. To define this formally, we represent each tree node as the set of vertices associated with it. Thus, given a graph G = (V, E), a tree decomposition is a pair (X, T), where X = {X1, ..., Xn} is a family of subsets of V, and T is a tree whose nodes are the subsets Xi, satisfying the following properties[2]:
- The union of all sets Xi equals V. That is, each graph vertex is associated with at least one tree node.
- For every edge (v, w) in the graph, there is a subset Xi that contains both v and w. That is, vertices are adjacent in the graph only when the corresponding subtrees have a node in common.
- If Xi and Xj both contain a vertex v, then all nodes Xk of the tree in the (unique) path between Xi and Xj contain v as well. That is, the nodes associated with vertex v form a connected subset of T. This is also known as coherence, or the running intersection property. It can be stated equivalently that if
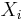 ,
, 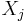 and
and 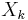 are nodes, and
are nodes, and 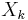 is on the path from
is on the path from 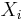 to
to 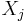 , then
, then 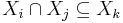 .
.
The tree decomposition of a graph is far from unique; for example, a trivial tree decomposition contains all vertices of the graph in its single root node.
Treewidth
The width of a tree decomposition is the size of its largest set Xi minus one. The treewidth tw(G) of a graph G is the minimum width among all possible tree decompositions of G. In this definition, the size of the largest set is diminished by one in order to make the treewidth of a tree equal to one. Equivalently, the treewidth of G is one less than the size of the largest clique in the chordal graph containing G with the smallest clique number. The graphs with treewidth at most k are also called partial k-trees.
It is NP-complete to determine whether a given graph G has treewidth at most a given variable k.[3] However, when k is any fixed constant, the graphs with treewidth k can be recognized, and a width k tree decomposition constructed for them, in linear time.[4] The time dependence of this algorithm on k is exponential.
Treewidth may also be characterized in terms of havens, functions describing an evasion strategy for a certain pursuit-evasion game defined on a graph. A graph G has treewidth k if and only if it has a haven of order k + 1 but of no higher order, where a haven of order k + 1 is a function β that maps each set X of at most k vertices in G into one of the connected components of G \ X and that obeys the monotonicity property that β(Y) ⊆ β(X) whenever X ⊆ Y.[5]
Graph minors
For any fixed constant k, the partial k-trees are closed under the operation of graph minors, and therefore, by the Robertson–Seymour theorem, this family can be characterized in terms of a finite set of forbidden minors. For partial 1-trees (that is, forests), the single forbidden minor is a triangle, and for the partial 2-trees the single forbidden minor is the complete graph on four vertices. However, the number of forbidden minors increases for larger values of k: for partial 3-trees there are four forbidden minors, the complete graph on five vertices, the octahedral graph with six vertices, the eight-vertex Wagner graph, and the pentagonal prism with ten vertices.[6]
The planar graphs do not have bounded treewidth, because the n × n grid graph is a planar graph with treewidth n. Therefore, if F is a minor-closed graph family with bounded treewidth, it cannot include all planar graphs. Conversely, if some planar graph cannot occur as a minor for graphs in family F, then there is a constant k such that all graphs in F have treewidth at most k. That is, the following three conditions are equivalent to each other:[7]
- F is a minor-closed family of bounded-treewidth graphs;
- One of the finitely many forbidden minors characterizing F is planar;
- F is a minor-closed graph family that does not include all planar graphs.
Families of graphs with bounded treewidth include the cactus graphs, pseudoforests, series-parallel graphs, outerplanar graphs, Halin graphs, and Apollonian networks.[6] The control flow graphs arising in the compilation of structured programs also have bounded treewidth, which allows certain tasks such as register allocation to be performed efficiently on them.[8]
Dynamic programming
At the beginning of the 1970s, it was observed that a large class of combinatorial optimization problems defined on graphs could be efficiently solved by non serial dynamic programming as long as the graph had a bounded dimension,[9] a parameter related to treewidth. Later, several authors independently observed at the end of the 1980s[10] that many algorithmic problems that are NP-complete for arbitrary graphs may be solved efficiently by dynamic programming for graphs of bounded treewidth, using the tree-decompositions of these graphs.
As an example, consider the problem of finding the maximum independent set in a graph of treewidth k. To solve this problem, first choose one of the nodes of the tree decomposition to be the root, arbitrarily. For a node Xi of the tree decomposition, let Di be the union of the sets Xj descending from Xi. For an independent set S ⊂ Xi, let A(S,i) denote the size of the largest independent subset I of Di such that I ∩ Xi = S. Similarly, for an adjacent pair of nodes Xi and Xj, with Xi farther from the root of the tree than Xj, and an independent set S ⊂ Xi ∩ Xj, let B(S,i,j) denote the size of the largest independent subset I of Di such that I ∩ Xi ∩ Xj = S. We may calculate these A and B values by a bottom-up traversal of the tree:
where the sum in the calculation of 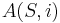 is over the children of node
is over the children of node 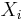 .
.
At each node or edge, there are at most 2k sets S for which we need to calculate these values, so if k is a constant then the whole calculation takes constant time per edge or node. The size of the maximum independent set is the largest value stored at the root node, and the maximum independent set itself can be found (as is standard in dynamic programming algorithms) by backtracking through these stored values starting from this largest value. Thus, in graphs of bounded treewidth, the maximum independent set problem may be solved in linear time. Similar algorithms apply to many other graph problems.
This dynamic programming approach is used in machine learning via the junction tree algorithm for belief propagation in graphs of bounded treewidth. It also plays a key role in algorithms for computing the treewidth and constructing tree decompositions: typically, such algorithms have a first step that approximates the treewidth, constructing a tree decomposition with this approximate width, and then a second step that performs dynamic programming in the approximate tree decomposition to compute the exact value of the treewidth.[4]
Treewidth of cliques
In any tree decomposition 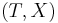 of a graph containing a clique there is a node i in T such that
of a graph containing a clique there is a node i in T such that 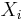 contains all the nodes of the clique. This is shown by induction on the size of the clique. The base cases are cliques of size 1 and 2, which follow from the conditions 1 and 2 on a tree decomposition. The inductive case is a graph containing a clique of size k+1, where k is 2 or greater. Let C be the set of nodes in the clique. Since
contains all the nodes of the clique. This is shown by induction on the size of the clique. The base cases are cliques of size 1 and 2, which follow from the conditions 1 and 2 on a tree decomposition. The inductive case is a graph containing a clique of size k+1, where k is 2 or greater. Let C be the set of nodes in the clique. Since 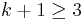 , there are at least three nodes in the clique, call them x, y and z. We know from the induction hypothesis that there are nodes a, b and c in the tree decomposition with
, there are at least three nodes in the clique, call them x, y and z. We know from the induction hypothesis that there are nodes a, b and c in the tree decomposition with
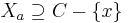 ,
, 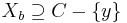 ,
, 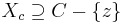 .
.
In a tree there is exactly one path between any two nodes. A second property of trees is that the three paths between a, b and c have a non-empty intersection. Let v be a node in this intersection. From condition 3 on a tree decomposition we get that
This implies that 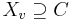 .
.
It follows from this that the treewidth of a k-clique is k-1.
Treewidth of trees
A connected graph with at least two vertices has treewidth 1 if and only if it is a tree. This can be shown in two steps, first that a tree has treewidth 1, second, that a connected graph with treewidth 1 is a tree.
To show the former, use induction on the number of vertices in the tree to show that it has a tree decomposition with no bag with size larger than two. The base case is a tree with two vertices, in which case the tree decomposition with one single node is sufficient. The inductive case is a tree  with
with 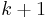 vertices, where
vertices, where  is any integer greater than
is any integer greater than 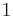 . If we remove a leaf
. If we remove a leaf  from the graph, we get a tree of size
from the graph, we get a tree of size  . From the induction hypothesis we can create a tree decomposition
. From the induction hypothesis we can create a tree decomposition 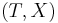 of width 1 of this graph. Let
of width 1 of this graph. Let  be the unique neighbour of
be the unique neighbour of  in
in  and
and  some node in
some node in  such that
such that  is in
is in 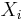 . Let
. Let 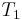 be
be  added a node
added a node  with
with  as its only neighbour and let
as its only neighbour and let 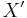 be
be  with the addition that
with the addition that 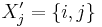 . Now
. Now 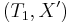 is a tree decomposition of
is a tree decomposition of  with width 1.
with width 1.
Now it remains to show that a connected graph with treewidth 1 is a tree. The contrapositive statement is that a graph with a cycle does not have treewidth 1. A graph with a cycle has the 3-clique as a minor, which from the statement in the previous section has treewidth 2. Since the partial 2-trees are closed under minors, the graph therefore has treewidth 2 or greater.
See also
- Clique-width
- Branch-decomposition, a closely related structure whose width is within a constant factor of treewidth
- Path decomposition, a tree decomposition in which the underlying tree of the decomposition is a path graph
- Cycle rank, a number that is bounded for a minor-closed graph family if and only if the family excludes a path
- Degeneracy, a measure of the sparsity of a graph that is at most equal to its treewidth
Notes
- ^ Diestel (2005) pp.354–355
- ^ Diestel (2005) section 12.3
- ^ Arnborg, Corneil & Proskurowski (1987).
- ^ a b Bodlaender (1996).
- ^ Seymour & Thomas (1993).
- ^ a b Bodlaender (1998).
- ^ Robertson & Seymour (1986).
- ^ Thorup (1998).
- ^ Bertelé (1972)
- ^ Arnborg & Proskurowski (1989); Bern, Lawler & Wong (1987); Bodlaender (1988).
References
- Arnborg, S.; Corneil, D.; Proskurowski, A. (1987), "Complexity of finding embeddings in a k-tree", SIAM Journal on Matrix Analysis and Applications 8 (2): 277–284, doi:10.1137/0608024.
- Arnborg, S.; Proskurowski, A. (1989), "Linear time algorithms for NP-hard problems restricted to partial k-trees", Discrete Applied Mathematics 23 (1): 11–24, doi:10.1016/0166-218X(89)90031-0.
- Bern, M. W.; Lawler, E. L.; Wong, A. L. (1987), "Linear-time computation of optimal subgraphs of decomposable graphs", Journal of Algorithms 8 (2): 216–235, doi:10.1016/0196-6774(87)90039-3.
- Bertelé, Umberto; Brioschi, Francesco (1972), Nonserial Dynamic Programming, Academic Press, ISBN 0120934507.
- Bodlaender, Hans L. (1988), "Dynamic programming on graphs with bounded treewidth", Proc. 15th International Colloquium on Automata, Languages and Programming, Lecture Notes in Computer Science, 317, Springer-Verlag, pp. 105–118, doi:10.1007/3-540-19488-6_110.
- Bodlaender, Hans L. (1996), "A linear time algorithm for finding tree-decompositions of small treewidth", SIAM Journal on Computing 25 (6): 1305–1317, doi:10.1137/S0097539793251219.
- Bodlaender, Hans L. (1998), "A partial k-arboretum of graphs with bounded treewidth", Theoretical Computer Science 209 (1–2): 1–45, doi:10.1016/S0304-3975(97)00228-4.
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6, http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/.
- Halin, Rudolf (1976), "S-functions for graphs", Journal of Geometry 8: 171–186.
- Robertson, Neil; Seymour, Paul D. (1984), "Graph minors III: Planar tree-width", Journal of Combinatorial Theory, Series B 36 (1): 49–64, doi:10.1016/0095-8956(84)90013-3.
- Robertson, Neil; Seymour, Paul D. (1986), "Graph minors V: Excluding a planar graph", Journal of Combinatorial Theory, Series B 41 (1): 92–114, doi:10.1016/0095-8956(86)90030-4.
- Seymour, Paul D.; Thomas, Robin (1993), "Graph Searching and a Min-Max Theorem for Tree-Width.", Journal of Combinatorial Theory, Series B 58 (1): 22–33, doi:10.1006/jctb.1993.1027.
- Thorup, Mikkel (1998), "All structured programs have small tree width and good register allocation", Information and Computation 142 (2): 159–181, doi:10.1006/inco.1997.2697.